Subtracting mixed numbers with regrouping can be super tricky for some (or most) students. There are many ways to teach subtracting mixed numbers with regrouping using manipulatives that may help your students conceptualize the process. On this post, Rachel from You’ve Got This Math will share three of her favorite ways to teach subtracting mixed numbers when borrowing is necessary.

Subtracting Mixed Numbers with Regrouping Using Manipulatives – Pattern Blocks
Pattern blocks are a simple way to build fraction sense, and if your students are already familiar with using them for fractions, then this is a wonderful place to start when teaching subtracting mixed numbers with regrouping using manipulatives.
Let’s say we have the subtraction problem 3 – 1 1/3. It may seem complicated to students at first. You can’t subtract 1/3 from 0, so you have to regroup and get a fraction from the 3. For some students, it is overwhelming. But it doesn’t have to be, especially if you use pattern blocks to model the process.
Here’s how to do it.
- Start by looking at the number you will be subtracting from, and lay that out in front of you. (Most of the time when using pattern blocks the whole is a hexagon. You can change that, but for today we will always assume that the hexagon equals one whole). Since I’m subtracting from 3, I’m going to lay out three hexagons in front of me.

2. Now it is time to subtract. The first thing I want to do is take away 1/3, but I can’t do this because all I have are three wholes. If your students have played with pattern blocks, then they should know that the rhombus equals 1/3 of a hexagon. So we are going to replace (we are really regrouping here) a hexagon with three rhombuses.

Finally, I can subtract. I take away 1/3 – one rhombus. Then, I take away 1 whole – 1 hexagon.

3. And the answer is… All that is left to do is to figure out the fraction that the leftover pattern blocks represent. There are 2 rhombuses, so I have 2/3, and there is one hexagon, so I have 1. The answer to 3 – 1 1/3 is 1 2/3.
Subtracting with Fraction Bars
I love fraction bars, or fraction tower cubes, because it is easy to explore fractions with the denominators 2 to 12. Pattern blocks limit the denominator that can be used, but you don’t have those limitations with fraction bars. The downside is that in each set, there are only enough fraction bars for one whole. So, to use them for subtracting mixed numbers, you need to have partners so that there are two sets of fraction bars for each set of students to use.
There are also programs online that allow children to use manipulatives to solve problems. Kidspiration is one I really enjoyed using…and you can use as many fraction bars as you need.
So, how do you use fractions bars or fraction tower cubes? Let’s give a problem a try.
Our problem is 2 1/4 – 1 1/2. This problem is a little trickier, because now we have to deal with unlike denominators, but it is still manageable when we use fraction bars.
- Just like we did with pattern blocks, we start by laying out the fraction bars that we will be subtracting from. We will grab two wholes and 1/4.

2. Depending on how deep you want to get with your students at this point in instruction, you can do this step or skip it. If you want to set up the premises for how they would solve a subtracting mixed numbers without manipulatives, you may want to do it. This step involves getting the common denominator. Some of our kiddos will just know that four is our least common denominator, but others will need a little more support. This can be done by listing a few multiples of each denominator.
2: 2, 4, 6,
4: 4, 8, 12
Once they are listed, it is easy to see that the LCD (least common denominator) is 4. I don’t need to do anything with my 1/4, but the children need to aware that I will be subtracting 2/4 when we get to that step.
3. The third step is to regroup. To do this, I will take away one of my wholes and replace that with four fourths. I now have five-fourths, and I’m ready to subtract.

4. This part is the easiest. Simply take away one-half, or two-fourths, and then take away one whole.

If you didn’t have your children find the LCD, then all you need to do here is grab the 1/2 block and fill it up with as many fourths as you can – two, to be exact – and that is what they will subtract.

5. Finally, count up what is left. There are 0 whole bars and 3 fourths bars…so the answer is 3/4.
Subtracting with Area Models
This last one only requires two things: grid paper and colored pencils. Your artistic kiddos will love this method. The other benefit is that the only limitation is the size of the paper.
For this method, we will subtract 3 1/4 – 2 5/8.
- For this method, it is best if we find the LCD first.
4: 4, 8,12
8: 8, 16, 24
The least common denominator is 8, so we must find the equivalent fraction to 1/4 that has the denominator of 8.
1/4 x 2/2 = 2/8.
2. Now we can draw our area models. We know we need to draw three wholes, but we can’t forget about our two-eighths. So, we will actually need to draw four wholes, and based on our denominator, there will need to be eight parts in these wholes. The fun part with drawing models is that they can be drawn in numerous ways. We could draw a long rectangle that is 1 x 8, or we could draw a 2 x 4 rectangle. As long as there are eight squares in the rectangle, we are good to go.

3. Step 3 is to color in the area models to represent 3 2/8.

4. Subtracting time. Using a different colored pencil, we will cross off what we are subtracting. First, we cross off five-eights. It is important to let our students know to start with the area that only has two-eighths and then move to a model that is a whole.

Next, we cross off the two whole numbers. It is important to point out that we must cross off only our area models that equal one whole. Two of our models already have fractional parts crossed off. We can’t use those because they do not equal one whole.
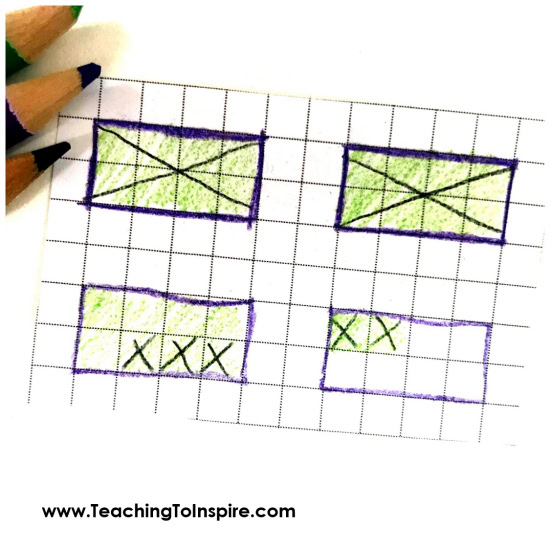
5. Finally, we count what is left. There are just five-eights left, so that is the answer.
Our children learn in so many different ways, so it is important to expose them to numerous ways. And to help you do this, we have three simple printables that allow your children to explore subtracting with regrouping using manipulatives.
Click here to grab the Subtracting with Mixed Numbers with Regrouping printables.
Next Steps for Subtracting Mixed Numbers with Regrouping
Once you are ready to move from manipulatives to abstract, I recommend using a pizza context to support the shift from manipulatives to equations and hand-drawn models.
If you are looking for a ready-made resource to help you make that move, then I recommend my Subtracting Mixed Numbers with Regrouping Using Pizza Resource, which you can see if you click here.
Guest Blogger: Rachel from You’ve Got This Math









Oh thanks for the blog post! My kids totally bombed this on our last test. I’m really excited to try the area models with them.
This year I discovered what I think is the *easiest* way to teach subtraction with mixed numbers, regardless of the denominator- open number lines and counting up. I struggled with how to make a useful strategy (like those presented above) with larger denominators (like 15). So this year we used open number lines and it made a huge difference! For example, if the problem was 10 1/3 – 8 4/5. we first talked about the common denominator. Then we started our open number line with 8 12/15 and talked about what we needed for our next whole. Once we got to 9, we talked about our next hop if our goal is 10 5/15. I started off the instruction using whole numbers to see how it works. Honestly, I don’t think I’ll teach subtracting mixed numbers any other way again!
I love this, Rachel! Thank you so much for sharing that strategy. I am going to have to try that.